I took some individual LEDs and soldered a resistor to them and then sealed and put heat-shrink on the leads.

Sidebar on LED resistors - skip to way down the page if you already know all this. I wrote this for a paper some time back.
=================================
Unlike incandescent light bulbs which light up due to a voltage across them, LED’s are primarily excited by electrical current. The brightness of the LED is directly proportional to the amount of current flowing through it (within limits).
The simplest discrete implementation of an LED light is using a current limiting resistor. LED’s cannot pass unlimited current through them, so a resistor (R) is needed to limit the amount of current flowing in the circuit.
Also important is that the LED has a positive side (anode) and a negative side (cathode). Current should always flow from the anode to the cathode.
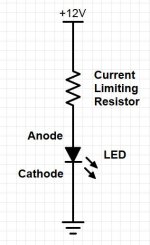
When choosing a discrete LED for a lighting application, two primary things must be known from the LED supplier. One is called forward voltage, or Vf. This is the amount of voltage difference that will be seen across the LED, regardless of the current through it (to a point). This number is usually somewhere between 2V and 3V for a single device. This number is important when calculating how big the current-limiting resistor should be.
The second parameter is the maximum continuous forward current allowed by the device. This number is typically 20mA for a single device.
So let’s get to some math. In the circuit shown above, there is current flowing from the 12V source to ground. There is a voltage drop, VR, across the current limiting resistor, and a voltage drop, VF, across the LED. These two voltage drops must add up to 12V (without considering the wires or connections).
The current flowing through all of the components in the system must be the same.
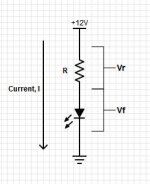
We have a formula, called Ohm’s law, that says V = I * R. This means that the voltage at any point in the circuit is the current that is flowing, times the resistance. We can use Ohm’s law to determine what the correct values are needed for our LED operation.
As an example, let’s say that you found out that your LED has a maximum forward current of 20mA. As stated above, since brightness is proportional to current, at this 20mA maximum current, the LED would be the brightest that it can be without damage. Let’s find out what the resistor value needs to be to light the LED with 20mA of current.
Let us also say that the manufacturer of the LED said that the forward voltage drop, Vf, was 2.2V.
Since the individual voltage drops across all elements in the system must add up to 12V in the above example, we can calculate what the voltage drop across the current limiting resistor (Vr) would be for the LED in operation: 12V – 2.2V = 9.8V.
We can then use Ohm’s law to find out what value the resistor needs to be to keep the LED from burning out. Rearranging V = I * R, gives R = V / I. We can then plug in our values and see that R = 9.8/0.02A = 490 Ohms.
A couple of generic, LED versions of Ohm’s law could be written as:
R = (Vsupply – VLEDforward) / I
and
I = (Vsupply – VLEDforward) / R
So for a maximum-brightness, 20mA, LED at 12V we need a 490 ohm current-limiting resistor. Great! We’re done!
But wait, what happens when your charger is plugged in and the supply voltage goes to 14, or even 15 volts?
If we put the numbers back into Ohms law with a 15V supply voltage, we see 15V – 2.2V (Vf) = 12.8V
Since we now have a fixed resistor in our system, rearranging V = I * R, gives I = V / R. This means that at 15V, the LED sees (15-2.2)/490 = 26mA! - a 30% increase of the specified limit. This LED will surely have a shortened life at these currents.
So what we really have to do, if we just want a cheap resistor for current-limiting, is to make our selection for the worst-case supply voltage. Rethinking things for a charging voltage that might go up to 15V, and then adding a bit of margin, we should really select Vsupply as 16V to be safe. In this case, the resistor should be R = (Vsupply – VLEDforward) / I, or (16-2.2)/0.02A = 690 ohms.
So, armed with our new resistor value, 690 ohms, we can calculate that the current through the LED (as mentioned above this is directly proportional to the brightness):
At 16V: I = (16-2.2) / 690 = 0.020 A
At 12V: I = (12-2.2) / 690 = 0.014 A
At 10V: I = (10-2.2) / 690 = 0.011 A
As you can see, in order to protect the LED from over current at system charging voltages, the LED brightness suffers by nearly 50% by the time your system battery is low.
LED’s give off different amounts of light (lumens) for a given amount of current depending on the quality of the LED and the manufacturer. You can experiment very cheaply with different LED types and different resistors using a simple multimeter.
So what did we get for all this? Well, if you don’t care so much about your lighting (accent, overhead, etc.) varying in brightness over the voltages of your system and the lowest brightness (caused by protection at high voltages) is acceptable to you, then you have a dirt-cheap way to get some LED lighting installed. A side benefit is they are very small, and can fit into some tiny places.
================================== [end sidebar]
So I took my made up LED's and drilled some selective holes in the cockpit coaming boxes and in the kickspace under the cabinets inside. I used some really cheesy wire since it is a non-critical "system", the currents are very small and it is easy to work with, not to mention cheap.
Here is one LED in the top corner of the coaming box:

The advantage of putting them in the top corner is that they are mostly out of the weather and sun. Here are some photos of what the coaming box LEDs look like:


Here is some wiring and one LED for the interior ones, poking down towards the sole.

Here is a photo of the LED underneath:

And here is what the interior LEDs look like. I use these for nightlights since they draw so little power.

Wow, looking back at the preview - sorry to ramble on and have taken up so much space!
Ray

Sidebar on LED resistors - skip to way down the page if you already know all this. I wrote this for a paper some time back.
=================================
Unlike incandescent light bulbs which light up due to a voltage across them, LED’s are primarily excited by electrical current. The brightness of the LED is directly proportional to the amount of current flowing through it (within limits).
The simplest discrete implementation of an LED light is using a current limiting resistor. LED’s cannot pass unlimited current through them, so a resistor (R) is needed to limit the amount of current flowing in the circuit.
Also important is that the LED has a positive side (anode) and a negative side (cathode). Current should always flow from the anode to the cathode.

When choosing a discrete LED for a lighting application, two primary things must be known from the LED supplier. One is called forward voltage, or Vf. This is the amount of voltage difference that will be seen across the LED, regardless of the current through it (to a point). This number is usually somewhere between 2V and 3V for a single device. This number is important when calculating how big the current-limiting resistor should be.
The second parameter is the maximum continuous forward current allowed by the device. This number is typically 20mA for a single device.
So let’s get to some math. In the circuit shown above, there is current flowing from the 12V source to ground. There is a voltage drop, VR, across the current limiting resistor, and a voltage drop, VF, across the LED. These two voltage drops must add up to 12V (without considering the wires or connections).
The current flowing through all of the components in the system must be the same.

We have a formula, called Ohm’s law, that says V = I * R. This means that the voltage at any point in the circuit is the current that is flowing, times the resistance. We can use Ohm’s law to determine what the correct values are needed for our LED operation.
As an example, let’s say that you found out that your LED has a maximum forward current of 20mA. As stated above, since brightness is proportional to current, at this 20mA maximum current, the LED would be the brightest that it can be without damage. Let’s find out what the resistor value needs to be to light the LED with 20mA of current.
Let us also say that the manufacturer of the LED said that the forward voltage drop, Vf, was 2.2V.
Since the individual voltage drops across all elements in the system must add up to 12V in the above example, we can calculate what the voltage drop across the current limiting resistor (Vr) would be for the LED in operation: 12V – 2.2V = 9.8V.
We can then use Ohm’s law to find out what value the resistor needs to be to keep the LED from burning out. Rearranging V = I * R, gives R = V / I. We can then plug in our values and see that R = 9.8/0.02A = 490 Ohms.
A couple of generic, LED versions of Ohm’s law could be written as:
R = (Vsupply – VLEDforward) / I
and
I = (Vsupply – VLEDforward) / R
So for a maximum-brightness, 20mA, LED at 12V we need a 490 ohm current-limiting resistor. Great! We’re done!
But wait, what happens when your charger is plugged in and the supply voltage goes to 14, or even 15 volts?
If we put the numbers back into Ohms law with a 15V supply voltage, we see 15V – 2.2V (Vf) = 12.8V
Since we now have a fixed resistor in our system, rearranging V = I * R, gives I = V / R. This means that at 15V, the LED sees (15-2.2)/490 = 26mA! - a 30% increase of the specified limit. This LED will surely have a shortened life at these currents.
So what we really have to do, if we just want a cheap resistor for current-limiting, is to make our selection for the worst-case supply voltage. Rethinking things for a charging voltage that might go up to 15V, and then adding a bit of margin, we should really select Vsupply as 16V to be safe. In this case, the resistor should be R = (Vsupply – VLEDforward) / I, or (16-2.2)/0.02A = 690 ohms.
So, armed with our new resistor value, 690 ohms, we can calculate that the current through the LED (as mentioned above this is directly proportional to the brightness):
At 16V: I = (16-2.2) / 690 = 0.020 A
At 12V: I = (12-2.2) / 690 = 0.014 A
At 10V: I = (10-2.2) / 690 = 0.011 A
As you can see, in order to protect the LED from over current at system charging voltages, the LED brightness suffers by nearly 50% by the time your system battery is low.
LED’s give off different amounts of light (lumens) for a given amount of current depending on the quality of the LED and the manufacturer. You can experiment very cheaply with different LED types and different resistors using a simple multimeter.
So what did we get for all this? Well, if you don’t care so much about your lighting (accent, overhead, etc.) varying in brightness over the voltages of your system and the lowest brightness (caused by protection at high voltages) is acceptable to you, then you have a dirt-cheap way to get some LED lighting installed. A side benefit is they are very small, and can fit into some tiny places.
================================== [end sidebar]
So I took my made up LED's and drilled some selective holes in the cockpit coaming boxes and in the kickspace under the cabinets inside. I used some really cheesy wire since it is a non-critical "system", the currents are very small and it is easy to work with, not to mention cheap.
Here is one LED in the top corner of the coaming box:

The advantage of putting them in the top corner is that they are mostly out of the weather and sun. Here are some photos of what the coaming box LEDs look like:


Here is some wiring and one LED for the interior ones, poking down towards the sole.

Here is a photo of the LED underneath:

And here is what the interior LEDs look like. I use these for nightlights since they draw so little power.

Wow, looking back at the preview - sorry to ramble on and have taken up so much space!
Ray
